RAYOS NOTABLES EN UN ESPEJO CONVEXO:

a)      todo rayo que incide en la dirección del centro de curvatura se refleja en la misma dirección

b)      todo rayo que incide en la  dirección del foco se refleja paralelo al eje principal

c)      todo rayo que incide paralelo al eje principal se refleja de tal forma que su prolongación pasa por el foco.

d)     Si dos rayos inciden paralelos, sus prolongaciones se intersectan en el plano focal. 

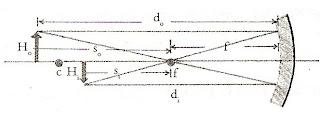
¿Como se forma la imagen de un objeto situado entre el infinito y el centro de curvatura?

Se traza un rayo luminoso (r₁) que incide paralelo al eje principal. Este rayo se refleja pasando por el foco

Se traza otro rayo ( r₂)  que incide pasando por el foco y refleja paralelo al eje principal. En el punto de intersección de los rayos reflejados se formara la imagen. Esta es real, menor e invertida.

¿Cómo se forma la imagen de un objeto situado en el centro de curvatura (d₀= r)?

·         Se dibuja el objeto en el centro de curvatura.

·         Se trazan dos rayos luminosos que pasen por el foco y se refleje paralelo al eje principal. En el punto donde se cortan los rayos reflejados se formara la imagen. Esta imagen es real, de igual tamaño e invertida. Haz la grafica.

¿Cómo se forma la imagen de un objeto situado entre el centro de curvatura y el foco (f < d₀ < r)?

·         Se dibuja el objeto entre el centro de curvatura y el foco

·         Se trazan dos rayos luminosos que pasen por el objeto: uno que incida paralelo al eje principal y se refleje paralelo al eje principal. Compruébalo gráficamente.

d₀₌Distancia objeto-espejo

d₁=Distancia imagen-espejo

s_o=Distancia objeto-foco

s₁=Distancia imagen-foco

h_o=Tamaño del objeto

 Tamaño de la imagen.

Como los triángulos son semejantes, establecemos la proporción entre los lados homólogos de los triángulos.

H₀/H₁=S₀/f=(1)

Observa que suponemos la curvatura muy pequeña: los triángulos mostrados también son semejantes:

H₀/H₁=f/ S₀=(2)

Al igualar las expresiones (1) y (2) obtenemos

S_o/f=f/s₁ Ósea s₀s₁= f²

Al remplazar a s₀=d₀-f, y s₁-d₁-f  la expresión queda (d₀-f) (d₁-f)=f  ²

Al multiplicar los binomios y cancelar f  ² tenemos:

1/f=1/d₀+₁/d₁

Expresión que se conoce con el nombre de formula de Descartes.

Se puede encontrar una nueva expresión estableciendo una proporción entre los triángulos semejantes mostrados:

H₀/H₁=d₀/d₁

Las magnitudes que se encuentran en el campo del espejo son positivas; las que se encuentran al otro lado son negativas.

Ejemplo: un objeto se coloca a 25 cm de un espejo cóncavo de 20 cm de distancia focal. Calcular grafica y analíticamente la posición de la imagen.

Solución grafica:

Solución analítica:

   D₀=25 cm

d₁=?

F=20 cm

1/f=1/d₀+1/d₁, de donde 1/d₁=1/f+1/d₀

Al remplazar 1/d₁=1/20cm+1/25cm=25cm-20cm/500cm²=5cm/500cm²

Por tanto  d₁=100cm

Como d₁<0 la imagen es real, mayor e invertida.

Ejemplo:

Calcular la distancia focal de un espejo, si se sabe de un objeto situado a una distancia de 24 cm se obtiene una imagen real, cuatro veces mayor.

d₀=24cm

d₁=?    H₁=4H₀

f=?

Al aplicar la proporción H₀/H₁=d₀/d₁   se encuentra el valor de d₁:

H₀/4H₀₌24km/d₁

d₁=24cm*4=96cm

Luego se aplica la formula de Descartes:

1/f=1/d₀+1/d_1; 1/f=1/24cm+1/96cm

1/f=4/96cm+1/96cm=51/96cm

Luego f=96/5=19,2cm

Un objeto se coloca a 12 cm de un espejo convexo de 8 cm de distancia focal, calcular la posición de la imagen, gráficamente y analíticamente.

Solución grafica:

d₀=12cm

f=8cm (al otro lado del campo del espejo)

d₁=?   

1/f=1/d₀+1/d₁

1/d₁=1/f+1/d₀

1/d₁=1/-8cm+12cm=-12cm-8cm/96m²

1/d₁=-20cm/96cm₂+1/12cm d´=-96cm²/20cm=4,8cm

Como d₁<0  la imagen virtual